1 + 2 + 3 + 4 + ⋯

1 + 2 + 3 + 4 + ⋯ — bu ketma-ket natural sonlar yigʻindisidan iborat sonlar qatori boʻlib, ketma-ket kelgan $n$-qismli yigʻindi uchburchak son boʻlsa, quyidagi oʻrinlidir:

$\sum _{k=1}^{n}k={\frac {n(n+1)}{2}}$ 

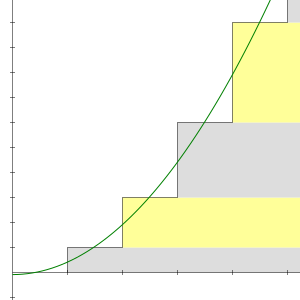
Bu yigʻindi cheksiz oʻsib boradi, chunki $n$ cheksizlikka intiladi. Yigʻindidan tashkil topgan ushbu ketma-ketlik, cheklangan chegaraga ega emas sanaladi.

Bir qarashda 1 + 2 + 3 + 4 + ⋯ ketma-ketligi hech qanday ahamiyatga ega emasdek tuyulsa-da, ularni bir qator matematik jihatdan qiziqarli natijalarga erishish maqsadida hisoblash mumkin. Masalan, matematikada sonlarni juftlashuvchi qatorlarga ajratish uchun koʻplab yigʻindini hisoblash usullari mavjud. Xususan, zeta funksiyasini tartibga solish usullari hamda Ramanujan yigʻindisi qatorni qiymatini belgilaydi, bu esa quyidagi mashhur formula bilan ifodalanadi:

$1+2+3+4+\cdots =-{\frac {1}{12}}$

Bu yerdagi tenglikdan chap tomon odatdagi cheksiz qator yigʻindisi sifatida emas, balki yuqoridagi yigʻindini hisoblash usullaridan biri yordamida olingan qiymat sifatida talqin qilinishi kerak. Ushbu usullar kompleks tahlil, kvant maydon nazariyasi hamda string nazariyasi kabi sohalarda qoʻllanilishini kuzatishimiz mumkin.

Adabiyotlar

• Zwiebach, Barton. A First Course in String Theory. Cambridge UP, 2004. ISBN 0-521-83143-1.  Qarang: s. 293.
• Elizalde, Emilio (2004). "Proceedings of the II International Conference on Fundamental Interactions". Proceedings of the II International Conference on Fundamental Interactions. 
• Watson, G. N. (April 1929), „Theorems stated by Ramanujan (VIII): Theorems on Divergent Series“, Journal of the London Mathematical Society, 1, 4 (2): 82–86, doi:10.1112/jlms/s1-4.14.82

Havolalar

• Lamb E. (2014), „1+2+3… chindan ham −1/12 ga tengmi?“, Scientific American bloglari.
  • John Baez. „Men yoqtirgan sonlar: 24“ (19-sentabr 2008-yil).