Uch oʻlchamli fazo
Uch o‘lchamli maydon -moddiy dunyoning geometrik modelidir. Bu fazo uzunlik, kenglik va balandlik bo’yicha uchta bir xil o'lchamga ega. Bu uch birlik ortogonal vektorlar bilan tavsiflanadi. Shuning uchun ham uch o‘lchovli maydon deb ataladi.

Insonning uch o‘lchamli fazo haqidagi tushunchasi uning go‘daklik davridayoq shakllanib boradi hamda hayoti davomida harakatlarini muvofiqlashtirishi bilan chambarchas bog‘liq sanaladi. Atrofdagi olamni sezgi organlari bilan uch o‘lchovda idrok etishning vizual qobiliyati chuqurlik idroki deb ataladi.
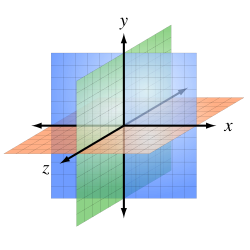
Analitik geometriyada uch o‘lchamli fazodagi har bir nuqta uchta kattalik - koordinatalar to‘plami sifatida ifodalanadi. Boshida kesishuvchi uchta o'zaro perpendikulyar koordinata o‘qi beriladi. Nuqtaning o‘rni shu uch o‘qga nisbatan tartiblangan uchlik sonlarni ko‘rsatish orqali beriladi. Ushbu raqamlarning har biri tegishli o‘q bo‘ylab o‘lchanadigan boshlang‘ich nuqtadan nuqtagacha bo‘lgan masofani ko‘rsatadi, bu nuqtadan boshqa ikkita o’q hosil qilgan tekislikgacha bo‘lgan masofaga teng bo’ladi.
Bundan tashqari, boshqa koordinata tizimlari ham mavjud bo‘lib, ular orasida silindrsimon va sferik tizimlar eng ko‘p qoʻllanadi.
Yana bir qarash chiziqli algebrada mavjud, ya’ni bu yerda chiziq mustaqilligi tushunchasi muhim rol o‘ynaydi. Maydon, qutining balandligi uning uzunligi va kengligiga bog'liq bo’lmaganligi sababli uch o'lchamli hisoblanadi. Chiziqli algebra tilida fazo uch o'lchovlidir.Chunki har bir nuqta uchta chiziqli mustaqil vektorlarning kombinatsiyasi bilan berilishi mumkin. Bu fazoviy atamalar bilan aytganda, to'rt o'lchovli, chunki nuqtaning vaqtdagi holati uning fazodagi holatiga bog'liq emas.
Uch o‘lchamli fazo uni boshqa o‘lchamdagi maydonlardan ajratib turadigan bir qancha xususiyatlarga ega. Masalan, bu eng kichik o‘lchamdagi maydon bo‘lib, unda siz arqonning bir qismiga tugun bog‘lashingiz mumkin[1]. Ko‘pgina fizika qonunlari, masalan, ko‘plab teskari kvadrat qonunlari bizning fazomizning o‘lchami uchta ekanligi bilan bog'liq[2].
Nol o‘lchamli, bir o‘lchamli va ikki o‘lchamli fazolarni uch o'lchamli fazoda joylashgan deb hisoblash mumkin. Uning o‘zini esa to‘rt o‘lchamli fazo modelining bir qismi deb hisoblash mumkin (to‘rtinchi o‘lchov ba’zan vaqt deb ataladi) [3] .
Manbalar
tahrir- ↑ Dale Rolfsen, Knots and Links, Publish or Perish, Berkeley, 1976, ISBN 0-914098-16-0
- ↑ Brian Greene, The Fabric of the Cosmos, Random House, New York, 2003, ISBN 0-375-72720-5
- ↑ „Четырёхмерное пространство — время“. Qaraldi: 2009-yil 26-fevral.